Uji Normalitas

Uji normalitas berguna untuk menentukan data yang telah dikumpulkan berdistribusi normal atau diambil dari populasi normal. Metode klasik dalam pengujian normalitas suatu data tidak begitu rumit. Berdasarkan pengalaman empiris beberapa pakar statistik, data yang banyaknya lebih dari 30 angka (n > 30), maka sudah dapat diasumsikan berdistribusi normal. Biasa dikatakan sebagai sampel besar.

Namun untuk memberikan kepastian, data yang dimiliki berdistribusi normal atau tidak, sebaiknya digunakan uji statistik normalitas. Karena belum tentu data yang lebih dari 30 bisa dipastikan berdistribusi normal, demikian sebaliknya data yang banyaknya kurang dari 30 belum tentu tidak berdistribusi normal, untuk itu perlu suatu pembuktian. uji statistik normalitas yang dapat digunakan diantaranya Chi-Square, Kolmogorov Smirnov, Lilliefors, Shapiro Wilk.

Metode Chi Square

(Uji Goodness Of Fit Distribusi Normal)

Metode Chi-Square atau X2 untuk Uji Goodness of fit Distribusi Normal menggunakan pendekatan penjumlahan penyimpangan data observasi tiap kelas dengan nilai yang diharapkan.

Keterangan :
X2 = Nilai X2
Oi = Nilai observasi
Ei = Nilai expected / harapan, luasan interval kelas berdasarkan tabel normal dikalikan N (total frekuensi) (pi x N)
N = Banyaknya angka pada data (total frekuensi)

Komponen penyusun rumus tersebut di atas didapatkan berdasarkan pada hasil transformasi data distribusi frekuensi yang akan diuji normalitasnya, sebagai berikut:

Keterangan :
Xi = Batas tidak nyata interval kelas
Z = Transformasi dari angka batas interval kelas ke notasi pada distribusi normal
pi = Luas proporsi kurva normal tiap interval kelas berdasar tabel normal
Oi = Nilai observasi
Ei = Nilai expected / harapan, luasan interval kelas berdasarkan tabel normal dikalikan N (total frekuensi) (pi x N)

Persyaratan Metode Chi Square (Uji Goodness of fit Distribusi Normal)
a. Data tersusun berkelompok atau dikelompokkan dalam tabel distribus frekuensi.
b. Cocok untuk data dengan banyaknya angka besar ( n > 30 )
c. Setiap sel harus terisi, yang kurang dari 5 digabungkan.

Signifikansi:
Signifikansi uji, nilai X2 hitung dibandingkan dengan X2 tabel (Chi-Square).
Jika nilai X2 hitung < nilai X2 tabel, maka Ho diterima ; Ha ditolak.
Jika nilai X2 hitung > nilai X2 tabel, maka maka Ho ditolak ; Ha diterima.

Contoh:
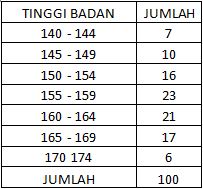
Diambil Tinggi Badan Mahasiswa Di Suatu Perguruan Tinggi Tahun 2010